Математичний маятник
Математичний маятник
Математичним маятником називають тіло невеликих розмірів, підвішене на тонкій нерозтяжній нитці, масою якої можна знехтувати, тобто вона мала в порівнянні з масою тіла.
У положенні рівноваги, коли маятник висить нерухомо, сила тяжіння врівноважується силою натягу нитки. При відхиленні маятника з положення рівноваги на деякий кут φ з'являється дотична складова сили тяжіння
Fτ = –mg sinφ . Знак «мінус» в цій формулі означає, що дотична складова направлена в бік, протилежний відхиленню маятника.
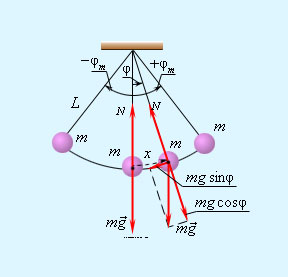 | |
Тільки в разі малих коливань, коли приблизно кут відхилення ( в радіанах) можна замінити на його сінус, математичний маятник є гармонійним осцилятором, тобто системою, здатною здійснювати гармонійні коливання.Практично таке наближення справедливе для кутів порядку 15–20°; при цьому величина кута відрізняється від його сінуса не більше ніж на 2 %.
Коливання маятника при великих амплітудах не є гармонійними.
![]()
І розв'язками цього рівняння будуть функції
|
Отримані функціїї є розв'язком основної задачі механіки для коливань математичного маятника. Координата змінюється по гармонійному (sin, cos) закону. Хm є максимальне значення координати, тобто максималне відхилення від положення рівноваги (амплітуда) Поточне значення координати залежить від велечини, що знаходиться під знаком сінуса або косінуса. Ця величина повинна мати зміст кута (цікаво - якого?), пропорційна часу, що пройшов з початку коливань і називається фазою.Саме фаза визначає стан коливальної системи в даний момент часу. Період коливань математичного маятника T = 2π√l /g.
|