Фізика 10 клас (Остапенко Т.М.)

РІВНЯННЯ СТАНУ ІДЕАЛЬНОГО ГАЗУ. РІВНЯННЯ МЕНДЄЛЄЄВА-КЛАПЕЙРОНА.

На минулих уроках ми розглянули випадки, коли один з трьох макропарметрів, які характеризують стан системи не змінюється. Ми вияснили, що якщо постійною є температура, то тиск і об'єм пов'язані законом Бойля-Маріотта, якщо постійний об'єм; то тиск і температура газу пов'язані законом Шарля; якщо постійний тиск, то об'єм і температура пов'язані законом Гей-Люссака.

Встановимо зв'язок між тиском, об'ємом і температурою деякої маси газу, коли змінюються усі три величини.

Нехай початковий об'єм, тиск і абсолютна температура деякої маси газу дорівнюють відповідно V₁, р₁ та Т₁, а кінцеві - відповідно V₂, р₂ та Т₂. Нехай перехід від першого стану до другого відбувався у два етапи. Припустимо, наприклад, спочатку змінився об'єм від V₁ до V₂, причому температура Т₁ залишалась без змін. Новий тиск газу, який він матиме в кінці цього процесу позначимо р. Другим етапом, змінювалась температура від  Т₁ до Т₂ при постійному об'ємі, при цьому тиск газу змінився від р до р₂. Випишемо в стовпчик величини, які характеризують кожен з трьох станів системи:

V₁, р₁, Т₁ - початковий (перший) стан системи І;

V₂, р, Т₁ - другий стан системи ІІ;

V₂, р₂, Т₂ - третій стан системи ІІІ;

Для переходу системи з стану І в стан ІІ застосуємо закон Бойля-Маріотта, оскільки даний процес є ізотермічним:

  звідки  (1)

Для переходу системи із стану ІІ в стан ІІІ застосуємо закон Шарля, оскільки даний процес є ізохоричним:

 (2)

Перемножимо рівняння (1) та (2) отримаємо:

 звідки  або  

Дане рівняння перепишемо в загальному вигляді, врахувавши, що значення V₁, р₁, Т₁ та V₂, р₂, Т₂ обрані довільним чином.

 або - рівняння Клапейрона

Такий самий висновок можна отримати використавши й іншу пару ізопроцесів. Спробуйте переконатись в цьому самостійно.

Отже, для даної маси газу добуток тиску газу на його об'єм пропорційний до абсолютної температури - це є рівняння Клапейрона.

Вдосконалив це рівняння відомий хімік Д.І. Менделєєв. Працюючи паралельно з Клапейроном він отримав таке ж рівняння. Крім того експериментально було встановлено, що  коефіцієнт пропорційності в даному рівнянні залежить від кількості речовини. Після усіх вдосконалень рівняння стану ідеального газу набуло вигляду:

- рівняння Мендєлєєва-Клапейрона (або рівняння стану ідеального газу)

де, m - маса газу;

 - молярна маса газу;

R - коефіцієнт пропорційності, який є однаковим для усіх газів і називається універсальною газовою сталою.

Вияснимо фізичний зміст універсальної газової сталої, для цього виразимо її з рівняння Менделєєва-Клапейрона.

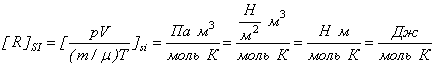
Отже,

Універсальна газова стала ([R]= )- це фізична величина, яка чисельно рівна роботі, яку потрібно виконати над ідеальним газом з кількість речовини 1 моль, щоб змінити його температуру на 1 кельвін.

Експериментальні дослідження показали, що R=8,314

ЦІКАВО ЗНАТИ

Рівняння стану - є узагальненим рівняння для всіх трьох раніше отриманих нами газових законі. Слід наголосити, що розв'язуючи будь-яку фізичну задачу, рівняння стану слід записати для КОЖНОГО з станів в яких перебуває система.

Покажемо, що з рівняння Мендєлєєва-Клапейрона можна отримати усі газові закони.

Нехай ідеальний газ, з незмінною кількістю речовини  в початковому стані характеризується макропараметрами V₁, р₁ та Т₁, а в кінцевому стані - відповідно V₂, р₂ та Т₂.

ІЗОТЕРМІЧНИЙ ПРОЦЕС, тобто Т₁= Т₂. Запишемо рівняння стану ідеального газу для двох станів:

Для стану І - (1)

Для стану ІІ - (2)

Оскільки у рівняннях (1) та (2) праві частини рівні, то й праві частини рівні, тоді можна записати, що  - ми отримали закон Бойля-Маріотта.

ІЗОБАРИЧНИЙ ПРОЦЕС, тобто р₁= р₂. Запишемо рівняння стану ідеального газу для двох станів:

Для стану І - (3)

Для стану ІІ - (4)

Поділимо рівняннях (3) на (4) , тоді

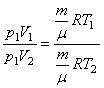  звідки  або V~T.  Ми отримали закон Гей-Люссака

ІЗОХОРИЧНИЙ ПРОЦЕС, тобто V₁= V₂. Запишемо рівняння стану ідеального газу для двох станів:

Для стану І - (5)

Для стану ІІ - (6)

Поділимо рівняннях (5) на (6) , тоді

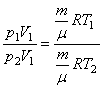  звідки  або р~T.   Ми отримали закон Шарля