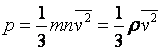Основне рівняння МКТ
Основне рівняння молекулярно-кінетичної теорії газів
На попередньому уроці ми вже з'ясували природу виникнення тиску газу. Але це було лише, так би мовити, якісне пояснення. Мета цього уроку - знайти залежність між величинами, які описують рух молекул газу та його тиском. Тиск, як відомо - це сила, що діє на одиницю площі поверхні. Отже, знаючи площу поверхні, наприклад, стінки посудини, нам залишиться лише обчислити силу, з якою діє молекула під час удару.
Розглянемо удар однієї окремої молекули о стінку посудини.
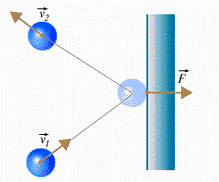
Газ у посудині - ідеальний. Отже, удари молекул є абсолютно пружними. Очевидно, що змінюється лише складова швидкості, перпендикулярна до стінки. При чому вона лише змінює свій напрям на протилежній, залишаючись за модулем сталою. А там де є зміна швидкості, є і зміна імпульсу. А це в свою чергу призводить до імпульсу сили, тобто добутку сили на час її дії:
Звичайно, тривалість удару однієї молекули дуже мала. Але, якщо врахувати, що одночасно о стінку вдаряється велика їх кількість, то можна припустити, що сила діє рівномірно впродовж певного періоду часу.
Отже, зміну імпульсу однієї молекули можна знайти за формулою:
Загальна ж зміна імпульсу становить
, де Z - кількість молекул, що змінили свій імпульс, тобто ті, що вдарилися о стінку.
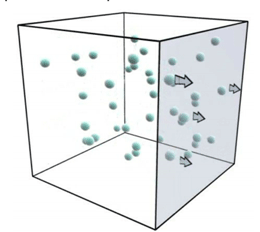
Обчислимо цю кількість молекул. Для цього обмежимо певну частину газу паралелепіпедом.
Z=p/2mvк
Розглянемо період часу Dt. Довжина нижнього ребра така, що молекули, які знаходяться лівіше не встигають долетіти до стінки за цей час. Іншими словами, вони не впливають на тиск у цей проміжок часу. Довжина цього ребра рівна l=vxDt, де - проекція швидкості молекул на вісь Ох.
Об'єм даного паралелепіпеда є добутком площі замальованої стінки S на довжину ребра l:
Загальна кількість молекул у даному об'ємі легко виразити через концентрацію n:
За імовірністю лише половина молекул буде летіти в напрямі стінки. Отже:
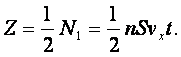
Вираз для зміни імпульсу набуває такого вигляду:
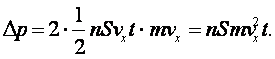
Отже,
А звідси:
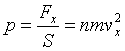
З тих самих міркувань отримаємо такі вирази для інших стінок:
Додавши ці рівності і розділивши на три ліву і праву частини отримаємо:
р=1/3 mv2
Вираз у дужках можна замінити на середній квадрат швидкості молекул, тобто:
Виведене рівняння називають основним рівнянням молекулярно-кінетичної теорії газів. Воно є дійсно важливим. Адже саме це рівняння встановлює зв'язок між мікро- і макросвітом. Адже в лівій частині цього виразу величина макроскопічна, тобто вимірювана, а в правій - мікроскопічні величини, які характеризують кожну газ із молекулярної точки зору.
Це рівняння можна дещо перетворити відносно початкового вигляду. Зокрема поділивши і помноживши праву частину рівняння на 2 і замінивши концентрацію, отримаємо:
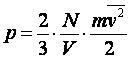
Вираз ![]() , є ніщо інше, як середня кінетична енергія руху молекул -
, є ніщо інше, як середня кінетична енергія руху молекул - ![]() .
.
Дістанемо:
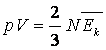
Можна зробити і такі перетворення: добуток концентрації молекул на їх масу - це густина газу. Отже: