Приклади розв'язування задач на рух тіла, кинутого під кутом до горизонту
РУХ ТІЛА, КИНУТОГО ПІД КУТОМ ДО ГОРИЗОНТУ
Задача № 1
Тіло кидають під кутом 300 до горизонту з початковою швидкістю 40 м/с. Знайдіть час польоту тіла. Визначте дальність польоту тіла та його максимальну висоту підняття. Знайдіть час підйому та опускання тіла.
Розв'язання:
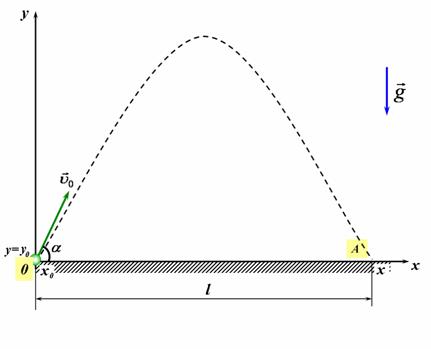
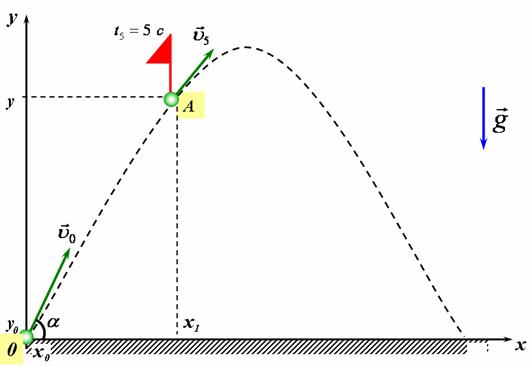
| 1) Побудуємо схему руху, пов'язавши систему відліку з землею. На рисунку 1 та 2 зображена траєкторії руху тіл. 2) Оскільки рух відбувається у площині, то для його описання потрібно взяти дві взаємо перпендикулярні осі координат OX таOY. 3) Для полегшення розв'язку задачі вважатимемо, що вісь координат ОY напрямлена вертикально вгору, а вісь OX - горизонтальна і направлена вздовж руху тіла, та в момент часt0=0 тіло знаходились в точці перетину осей, тобто в початку координат. |
40 м/с
-?
-?
І. ЗНАЙДЕМО ДАЛЬНІСТЬ ПОЛЬОТУ ТІЛА. ЧАС ПОЛЬОТУ ТІЛА:
На схемі руху позначимо початкову та кінцеву координати, вектори початкової, кінцевої швидкості та прискорення тіла (рис 1).
рис1 |
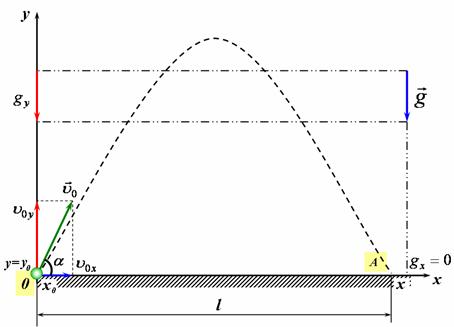
4) Спроектуємо зазначені вектори на вісь (рис 2).
рис2 |
5) Для знаходження дальності польоту тіла l запишемо рівняння руху для тіла в проекціях на осі координат від моменту, коли тіло почало рух, до моменту його падіння на землю:
Вісь ОХ
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
| Вісь OY
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
|
В рівнянні (2) скоротимо на час польоту t та знайдемо цей час:
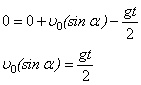
(*3) - час польоту тіла до падіння на землю.
Підставимо (3) в (1):
З математики відомо, що 
, тоді:
(*4) дальність польоту тіла
ЦІКАВО ПРОАНАЛІЗУВАТИ ОТРИМАНЕ СПІВВІДНОШЕННЯ:
З співвідношення (*4) слідує, що дальність польоту буде максимальною, при
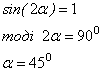
При 450 максимально можлива дальність польоту при фіксованому значенні 
буде дорівнювати:
ІІ. МАКСИМАЛЬНА ВИСОТА ПІДНЯТТЯ. ЧАСП ПІДЙОМУ ТА СПУСКУ:
Час підйому - це час, протягом якої тіло рухатиметься від точки кидання до найвищої точки траєкторії.
Час спуску - це час, протягом якого тіло рухатиметься від найвищої точки траєкторії до поверхні землі.
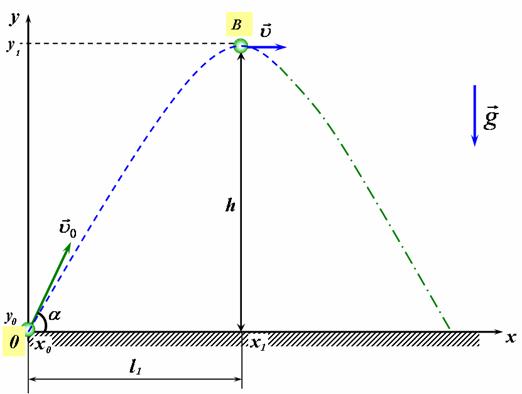
Складемо схему руху для випадку руху тіла від моменту кидання до найвищої точки траєкторії (рис 3):
рис 3 |
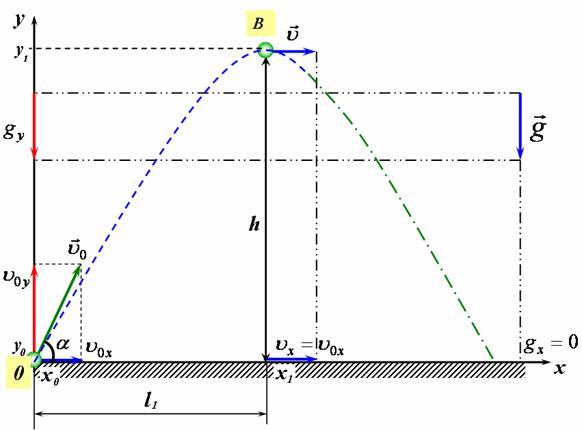
Спроектуємо вектори швидкості та прискорення на осі координат (рис 4):
рис 4 |
Запишемо рівняння руху для переміщення тіла з точки А до найвищої точки траєкторії, точки В, в проекціях на вісь OY:
- час підйому;
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
(5)
Запишемо рівняння швидкості для переміщення тіла з точки А до найвищої точки траєкторії, точки В, в проекціях на вісь OY:
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого випадку руху:
Підставимо відповідні значення в рівняння швидкості:
(6)
З рівняння (6) знайдемо час підйому :
(*7) - час підйому
Якщо час підйому порівняти з загальним часом руху (формула (*3)), то можна зробити висновок, що час підйому вдвічі менше за весь час руху, а отже час підйому дорівнюватиме часу спуску.
Підставимо (*7) в (*6):
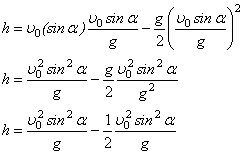
(*8) максимальна висота підняття тіла.
ЦІКАВО ПРОАНАЛІЗУВАТИ ОТРИМАНЕ СПІВВІДНОШЕННЯ:
З співвідношення (*8) слідує, що дальність польоту буде максимальною, при
При 900 максимально можлива дальність польоту при фіксованому значенні буде дорівнювати:
Перевіримо розмірність:
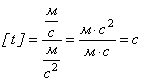
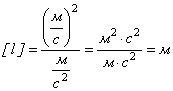
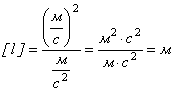
Виконаємо обчислення:
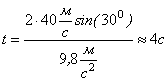
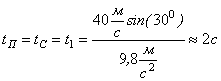
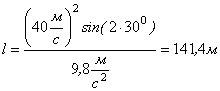
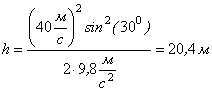
Відповідь: 
; 
; 
; 
Задача № 2
З гармати вистрілили снарядом. Швидкість снаряду =200 м/с, ствол гармати розташований під кутом 
=600 до горизонту. Знайдіть швидкість тіла через 5 с від моменту кидання.
Розв'язання:
| 1) Побудуємо схему руху, пов'язавши систему відліку з землею. На рисунку 1 та 2 зображена траєкторії руху тіл. 2) Оскільки рух відбувається у площині, то для його описання потрібно взяти дві взаємо перпендикулярні осі координат OX таOY. 3) Для полегшення розв'язку задачі вважатимемо, що вісь координат ОY напрямлена вертикально вгору, а вісь OX - горизонтальна і направлена вздовж руху тіла, та в момент часt0=0 тіло знаходились в точці перетину осей, тобто в початку координат. |
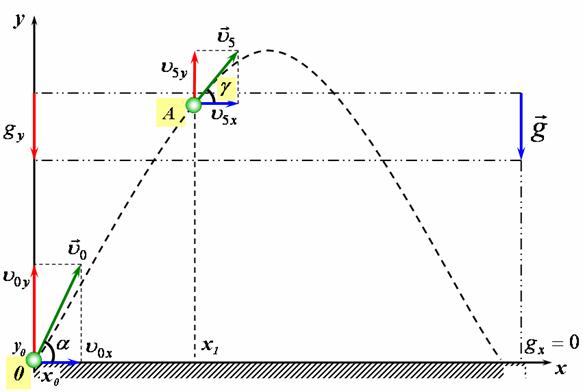
-? 3) Складемо схему руху для випадку руху тіла від моменту кидання до моменту падіння (рис 1) Вважатимемо, що в момент часу
=5 c тіло буде знаходиться в точці А:
рис 1 |
Спроектуємо вектори швидкості та прискорення на осі координат (рис 2):
рис 2 |
Запишемо рівняння швидкості для переміщення тіла з точки О до точки А за час 
, в проекціях на вісь OY та на вісь ОХ:
Вісь ОХ
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
| Вісь OY
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
|
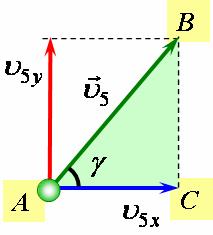
Тоді модуль швидкості 
можна знайти за теоремою Піфагора з утвореного трикутника 
:
 |
Підставивши в останнє рівняння замість сторін трикутника значення довжин проекцій та модуль вектора, отримаємо:
(3)
Підставимо (2) та (1) в (3):
(*4)
Оскільки швидкість - це векторна величина, то крім величини характеризується ще й напрямком. Напрямок можна вказати з допомогою значення кута, який утворює даний вектор з осями координат 
.Знайдемо цей кут з :
(5)
Підставимо (1) та (2) в (5):
Виконаємо обчислення:
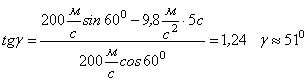
Відповідь: 
; 