2 Приклади розв'язування задач на вільне падіння
ВІЛЬНЕ ПАДІННЯ
Задача № 1
Тіло вільно падає з висоти 200 м. Знайдіть час падіння тіла. Знайдіть швидкість в момент падіння на землю, та через 2 свід початку падіння.
Розв'язання:
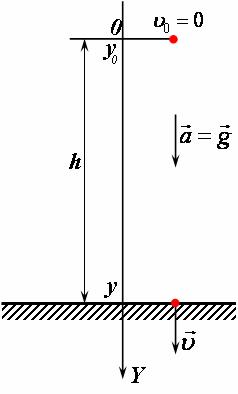
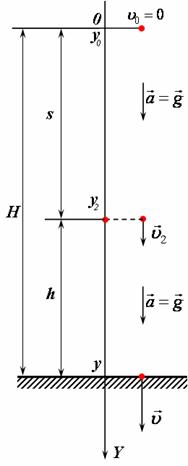
| 1) Побудуємо схему руху, пов'язавши систему відліку з землею. 2) Оскільки даний рух є рівноприскореним, то він складається з однієї ділянки, яку ми опишемо, використовуючи закони рівнозмінного руху. 3) Для полегшення розв'язку задачі вважатимемо, що вісь координатОY напрямлена вздовж руху тіла вертикально вниз, перпендикулярно до поверхні землі, та в момент час t=0 тіло знаходилось в початку координат, на висоті h над поверхнею землі. На схемі руху позначимо початкову та кінцеву координати, вектори початкової, кінцевої швидкості та прискорення (рис 1). |
=0
=2 с
-?
-?
рис1 |
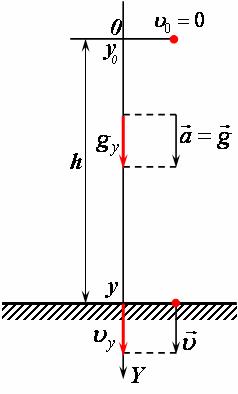
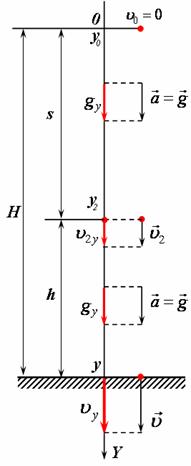
рис2 |
4) Спроектуємо зазначені вектори на вісь (рис 2).
5) Для знаходження шуканих величин запишемо рівняння руху та швидкості для даного руху в проекціях на обрану вісь ОY.Врахуємо, що рух відбувається з постійним прискоренням - прискоренням вільного падіння g:
Рівняння руху в загальному вигляді:
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
(1)
Рівняння швидкості в загальному вигляді:
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого випадку руху:
Підставимо відповідні значення в рівняння швидкості:
(2)
Отримали систему рівнянь з двома невідомими :
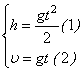
6) Розв'яжемо отриману систему рівнянь відносно шуканих невідомих:
Підставивши в рівняння швидкості (2) час 
знайдемо швидкість тіла через дві секунди від початку падіння:
(*3)
З рівняння (1) знайдемо час падіння:
(*4)
Підставимо рівняння (*4) в (2) знайдемо швидкість тіла в момент падіння на землю:
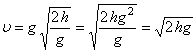(*5)
Перевірка розмінностей:
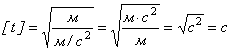
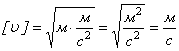
Виконаємо обчислення:
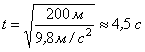
Відповідь:
; 
; 
Задача № 2
З даху будинку одна за одною падають дві краплі. Через час 2 с після початку падіння другої краплі відстань між ними дорівнювала 25 м. На скільки перша крапля відірвалась раніше від даху, ніж друга?
Розв'язання:
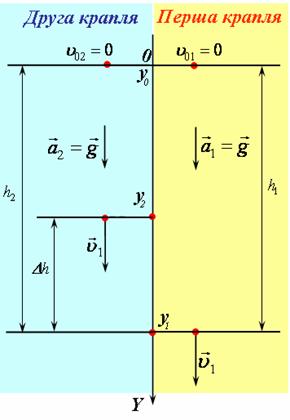
| 1) Побудуємо схему руху кожної краплі в одній системі координат, пов'язавши систему відліку з землею. 2) Оскільки рух кожної краплі є рівноприскореним, то він складається з однієї ділянки, яку ми опишемо, використовуючи закони рівнозмінного руху. 3) Для полегшення розв'язку задачі вважатимемо, що вісь координат ОY напрямлена вздовж руху тіла вертикально вниз, перпендикулярно до поверхні землі, та в момент час t=0 обидва тіла знаходилось в початку координат, на однаковій висоті над поверхнею землі і в момент часу |
=25 м
рис1 |
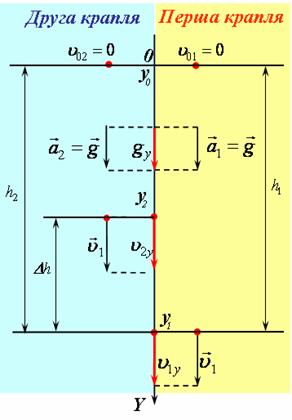
рис2 |
4) Спроектуємо зазначені вектори на вісь (рис 2).
5) Для знаходження шуканих величин запишемо рівняння руху та швидкості для руху кожної з крапель в проекціях на обрану вісьОY. Врахуємо, що рух кожної краплі відбувається з постійним прискоренням - прискоренням вільного падіння g:
Рівняння руху в загальному вигляді:
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Перша крапля
| Друга крапля
|
Підставимо відповідні значення в рівняння руху:
|
|
З рисунка 2 та рис 1 видно, що
(3)
Підставимо формули (1) та (2) в (3):
6) Розв'яжемо отриману дане рівняння відносно невідомої величини 
:
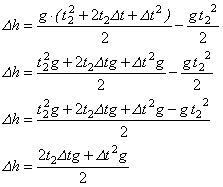
Ми отримали квадратне рівняння відносно , яке перепишемо у більш зручному вигляді:
Розв'яжемо це квадратне рівняння:
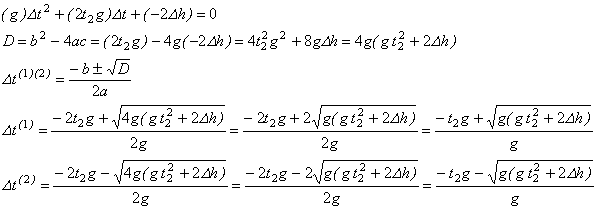
Корінь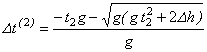 
є від'ємним, а тому не задовольняє умову задачі.
Отже,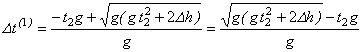 
(*)
Перевірка розмінності:
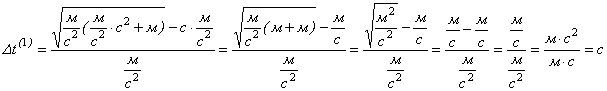
Виконаємо обчислення:
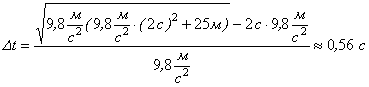
Відповідь: 
.
Задача № 3
В останню секунду вільного падіння тіло пройшло шлях 10 м. З якої висоти падало тіло?
Розв'язання:
| 1) Побудуємо схему руху, пов'язавши систему відліку з землею. 2) Оскільки даний рух є рівноприскореним, то він складається з однієї ділянки, яку ми опишемо, використовуючи закони рівнозмінного руху. 3) Для полегшення розв'язку задачі вважатимемо, що вісь координатОY напрямлена вздовж руху тіла вертикально вниз, перпендикулярно до поверхні землі, та в момент час t=0 тіло знаходилось в початку координат, на висоті Н над поверхнею землі. |
=1 сРозіб'ємо шлях пройдений тілом до падіння на землю на дві ділянки:
Øшлях, пройдений тілом за весь час руху t;
Øшлях пройдений тілом за (t-1) секунди падіння;
3) Складемо схему руху тіла за весь час падіння та за час 
секунди (
)на одному рисунку. На схемі руху позначимо початкову та кінцеву координати, вектори початкової, кінцевої швидкості та прискорення руху, яке дорівнюватиме g (рис 1).
рис1 |
рис2 |
4) Спроектуємо зазначені вектори на вісь (рис 2).
5) Для знаходження шуканих величин запишемо рівняння руху та швидкості для даного руху в проекціях на обрану вісь ОY.Врахуємо, що рух відбувається з постійним прискоренням - прискоренням вільного падіння g:
Рівняння руху в загальному вигляді:
- шлях пройдений тілом за весь час падіння t;
- шлях пройдений тілом за секунди ();
- шлях пройдений тілом за останню секунду падіння;
Знайдемо шляхи та записавши відповідно рівняння руху для всього часу руху та для секунди в проекціях на обрану вісь ОY:
Рівняння руху для всього часу падіння t:
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
(1)
Рівняння руху, від моменту початку руху, для секунди падіння ():
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
(2)
Тоді, шлях пройдений тілом за останню секунду знайдемо як різницю шляхів за весь час падіння t та за секунду падіння ():
(3)
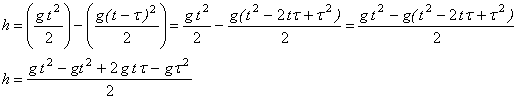
Підставимо (1) та (2) в (3):
(3)
З формули (3) знайдемо час падіння тіла:
(4)
Підставимо час падіння (4) у рівняння руху (1) та знайдемо висоту падіння:
(*)
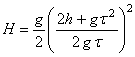
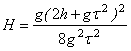
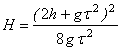Перевірка розмінності
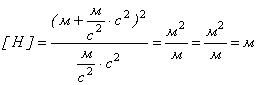
Виконаємо обчислення , врахувавши, що ():
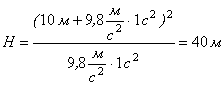
Відповідь: 