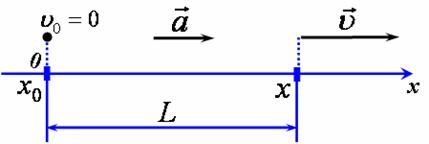2. Приклади розв'язування задач на рівноприскорений рух
ПРИСКОРЕННЯ. РІВНОЗМІННИЙ РУХ
Задача № 1
Автомобіль, рухаючись рівносповільнено зменшив свою швидкість від 20 м/с до 15 м/с за 2 с. Знайдіть прискорення автомобіля, та шлях, пройдений ним за час гальмування.
Розв'язання:
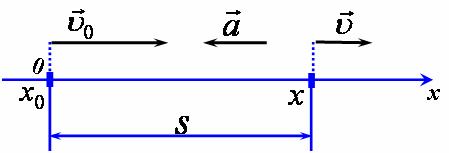
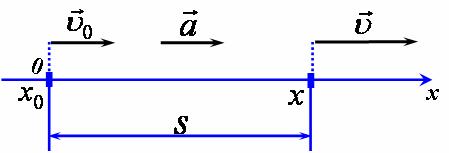
| 1) Побудуємо схему руху, пов'язавши систему відліку з землею. 2) Оскільки даний рух цілком є рівносповільненим, то він складається з однієї ділянки, яку ми опишемо, використовуючи закони рівнозмінного руху. 3) Для полегшення розв'язку задачі вважатимемо, що вісь координат ОХ напрямлена вздовж руху тіла, та в момент час t=0 тіло знаходилось в початку координат. На схемі руху позначимо початкову та кінцеву координати, вектори початкової, кінцевої швидкості та прискорення (рис 1).
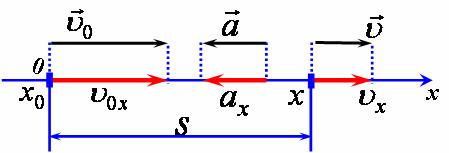
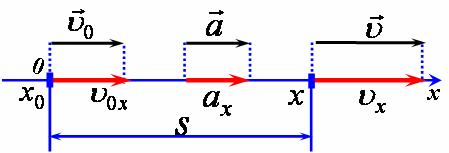
рис1 4) Спроектуємо зазначені вектори на вісь (рис 2).
рис2 |
5) Запишемо рівняння руху та швидкості для даного руху в проекціях на обрану вісь ОХ:
Рівняння руху в загальному вигляді:
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
(1)
Рівняння швидкості в загальному вигляді:
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого випадку руху:
Підставимо відповідні значення в рівняння швидкості:
(2)
Отримали систему рівнянь з двома невідомими s та a:
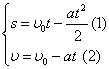
6) Розв'яжемо отриману систему рівнянь відносно шуканих невідомих:
З рівняння (2) знайдемо прискорення руху:
(3)
Підставимо рівняння (3) в (1): 
(*)
Підставимо в отриману кінцеву формулу значення:
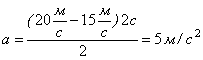
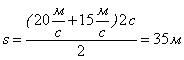
Відповідь: 
; 
Задача № 2
Під час розбігу із стану спокою літак збільшив свою швидкість до 50 м/с, пройшовши шлях 1000 м. Знайдіть прискорення літака та час розбігу.
Розв'язання:
| 1) Побудуємо схему руху, пов'язавши систему відліку з землею. 2) Даний рух є рівноприскореним. Розглянемо рух літака із стану спокою до моменту, коли його швидкість стала рівною 50 м/с. 3) Для полегшення розв'язку задачі вважатимемо, що вісь координат ОХ напрямлена вздовж руху тіла, та в момент час t=0 тіло знаходилось в початку координат. Складемо схему руху: на схемі руху позначимо початкову та кінцеву координати, вектори початкової, кінцевої швидкості та прискорення для кожної з ділянок (рис 1).
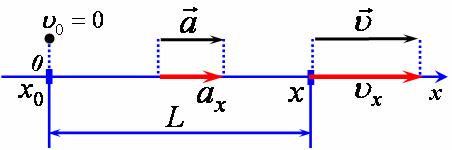
рис1 4) Спроектуємо зазначені вектори на вісь (рис 2).
рис2 |
-?
5) Запишемо рівняння руху та швидкості для даного руху в проекціях на обрану вісь ОХ:
Рівняння руху в загальному вигляді:
- час, за який літак проїде відстань L=1000 м.
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
(1)
Запишемо рівняння швидкості в загальному вигляді:
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого випадку руху:
Підставимо відповідні значення в рівняння швидкості:
(2)
Отримали систему рівнянь з двома невідомими t та a:
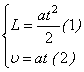
6) Розв'яжемо отриману систему рівнянь відносно невідомих та знайдемо прискорення руху літака a. З рівняння (2) знайдемо час розгону літака:
(3)
Підставимо рівняння (3) в (1): 
З отриманого рівняння знайдемо прискорення рівносповільненого руху літака:
(4)
Підставимо значення прискорення в рівняння (3):
(*)
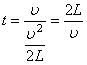Відповідь:
; 
Задача № 3
Прямий схил довжиною 100 м лижник пройшов за 20 с, рухаючись з прискоренням 0,3 м/с2. Яка швидкість лижника на початку та в кінці спуску? Знайдіть швидкість тіла через 5 с від початку руху.
Розв'язання:
| І. ЗНАЙДЕМО ШВИДКІСТЬ ЛИЖНИКА НА ПОЧАТКУ ТА В КІНЦІ СПУСКУ 1) Побудуємо схему руху, пов'язавши систему відліку з землею. 2) Оскільки даний рух цілком є рівноприскореним, то він складається з однієї ділянки, яку ми опишемо, використовуючи закони рівнозмінного руху. 3) Для полегшення розв'язку задачі вважатимемо, що вісь координат ОХ напрямлена вздовж руху лижника, та в момент час t=0 тіло знаходилось в початку координат. На схемі руху позначимо початкову та кінцеву координати, вектори початкової, кінцевої швидкості та прискорення (рис 1).
рис1 4) Спроектуємо зазначені вектори на вісь (рис 2).
рис2 |
-?
5) Запишемо рівняння руху та швидкості для даного руху в проекціях на обрану вісь ОХ:
Рівняння руху в загальному вигляді:
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
(1)
Рівняння швидкості в загальному вигляді:
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого випадку руху:
Підставимо відповідні значення в рівняння швидкості:
(2)
Отримали систему рівнянь з двома невідомими 
та 
:
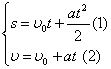
6) Розв'яжемо отриману систему рівнянь відносно шуканих невідомих:
З рівняння (1) знайдемо початкову швидкість :
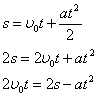
(*)(3)
Підставимо рівняння (3) в (2) та знайдемо кінцеву швидкість лижника :
(*)
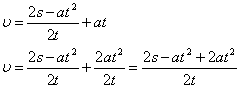
Підставимо в отриману кінцеву формулу значення:
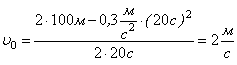
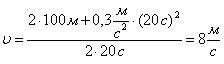
Перевірка розмірності:
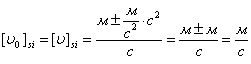
ІІ. ЗНАЙДЕМО ШВИДКІСТЬ ЛИЖНИКА ЧЕРЕЗ 5 с ВІД ПОЧАТКУ РУХУ.
1- 3 ) Побудуємо схему руху для перших п'яти секунд руху (
), пов'язавши систему відліку з землею. На схемі руху позначимо початкову та кінцеву координати, вектори початкової, кінцевої швидкості та вектор прискорення (рис 3).
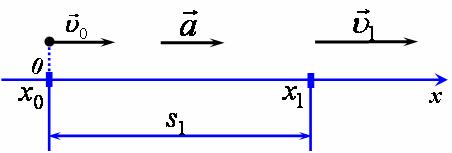
рис 3
4) Спроектуємо зазначені вектори на вісь (рис 2).
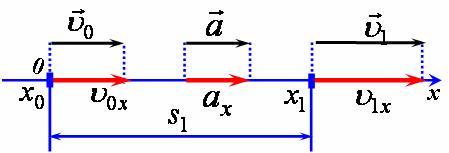
рис 4
Рівняння швидкості в проекціях на вісь ОХ для даної ділянки, яку пройшло тіло за час , рухаючись рівноприскорено 
має такий загальний вигляд:
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого випадку руху:
Підставимо відповідні значення в рівняння швидкості:
(4)
Підставимо в рівняння (4) значення початкової швидкості, формулу (*3):
(*5)
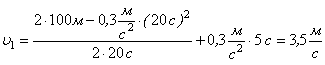
Відповідь:
; 
; 
.