Теорія по темі: "Повні квадратні рівняння"
Геометричний зміст
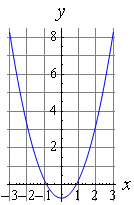Графіком квадратичної функції є парабола. Розв'язками (коренями) квадратного рівняння називають точки перетину параболи з віссю абсцис. Якщо парабола, яка описується квадратичною функцією, не перетинається з віссю абсцис, рівняння не має дійсних корнів. Якщо парабола перетинається з віссю абсцис в одній точці (вершині параболи), рівняння має один дійсний корінь (також кажуть, що рівняння має два співпадаючих кореня). Якщо парабола перетинає вісь абсцис в двох точках, рівняння має два дійсних кореня.
Якщо коефіцієнт а додатній, вітки параболи направлені вгору, якщо від'ємний -- вітки параболи направлені вниз. Якщо коефіцієнт b додатній, то вершина параболи лежить в лівій півплощині, якщо від'ємний -- в правій півплощині.
Вивід формули для розв'язання квадратного рівняння
Формулу для розв'язання квадратного рівняння можна отримати так
Помножимо рівняння на 4a
4a2x2 + 4abx = -4ac
4a2x2 + 4abx + b2 = -4ac + b2
(2ax + b)2 = b2 -4ac
2ax + b = ±√b2 -4ac
Пошук коренів квадратного рівняння
Квадратне рівняння з дійсними коефіцієнтами може мати від 0 до 2 дійсних коренів в залежності від значення дискримінанту D = b2 − 4ac:
- коли D > 0 корнів два, і вони розраховуються за формулою
x1,2 = -b ± √D 2a - коли D = 0 корінь один (два рівних або співпадаючих кореня), кратності 2:
x = -b 2a - коли D < 0 дійсних коренів немає. Існують два комплексних кореня, що розраховуються за формулою
x1,2 = -b ± i√-D 2a
Теорема Вієта
Сума коренів приведеного квадратного рівняння x2 + px + q = 0 дорівнює коефіцієнту p, взятому з оберненим знаком, а добуток коренів дорівнює вільному доданку q:
x1 + x2 = -p, x1x2 = q.
Розклад квадратного рівняння на множники
Якщо відомі обидва кореня квадратного рівняння, то його можна розкласти на множники за наступною формулою
ax2 + bx + c = a(x - x1)(x - x2)
7.4Мб