Основи алгоритмізації та програмування (Циммерман О.В.)

В конструктивную математическую логику А. А. Марков вводит понятие «разрешимое высказывание» и связанное с ним понятие «прямое отрицание». В логике А. А. Маркова имеется и другой вид отрицания — усиленное отрицание, относящееся к так называемым полуразрешимым высказываниям.

Кроме материальной и усиленной импликации, при установ­лении истинности которых приходится заботиться об истинности посылки и заключения, А. А. Марков вводит дедуктивную имп­ликацию, определяемую по другому принципу. Дедуктивная имп­ликация «если А, то В»выражает возможность выведения В из А по фиксированным правилам, каждое из которых в применении к верным формулам даст верные формулы. Всякое высказывание, выводимое из истинного высказывания, будет истинным.

Через дедуктивную импликацию А. А. Марков определяет редукционное отрицание (reductio ad absurdum). Редукционное отрицание высказывания А (сформулированного на данном язы­ке) понимается как дедуктивная импликация «если А, то Л», где через Л обозначен абсурд. Это определение отрицания соответ­ствует обычной практике рассуждений математика: математик отрицает ту посылку, из которой вытекает абсурд. Для установ­ления истинности редукционного отрицания высказывания не требуется вникать в смысл этого высказывания. Высказывание, для которого установлена истинность редукционного отрицания, не может быть истинным.

Аристо́тель (др.-греч. Ἀριστοτέλης; 384 до н. э., Стагира, Фракия — 322 до н. э., Халкида, остров Эвбея) — древнегреческий философ. Ученик Платона. С 343 до н. э. — воспитатель Александра Македонского^[1]. В 335/4 г. до н. э.^[2] основал Ликей (др.-греч.Λύκειον Лицей, или перипатетическую школу). Натуралист классического периода. Наиболее влиятельный из философов древности; основоположник формальной логики. Создал понятийный аппарат, который до сих пор пронизывает философский лексикон и стиль научного мышления.

Аристотель был первым мыслителем, создавшим всестороннюю систему философии, охватившую все сферы человеческого развития: социологию, философию, политику, логику, физику. Его взгляды на онтологию имели серьёзное влияние на последующее развитие человеческой мысли. Метафизическое учение Аристотеля было принято Фомой Аквинским и развито схоластическим методом. Карл Маркс называл Аристотеля величайшим мыслителем древности^[3].

Высказывание - это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).

Го́тфрид Ви́льгельм Ле́йбниц 

саксонский философ, логик,математик, механик, физик, юрист, историк, дипломат, изобретатель и языковед. Основатель и первый президент Берлинской Академии наук, иностранный член Французской Академии наук^[13].

Важнейшие научные достижения:

• Лейбниц, независимо от Ньютона, создал математический анализ — дифференциальное и интегральное исчисления (см. исторический очерк), основанные на бесконечно малых^[13].
• Лейбниц создал комбинаторику как науку^[14].
• Он заложил основы математической логики^[5][8].
• Описал двоичную систему счисления с цифрами 0 и 1^[15].
• В механике ввёл понятие «живой силы» (прообраз современного понятия кинетической энергии) и сформулировалзакон сохранения энергии^[5].
• В психологии выдвинул понятие бессознательно «малых перцепций» и развил учение о бессознательной психической жизни^[5].

Лейбниц также является завершителем философии XVII века и предшественником немецкой классической философии, создателем философской системы, получившей название монадология^[16]. Он развил учение об анализе и синтезе^[5][17], впервые сформулировал закон достаточного основания (которому, однако, придавал не только логический (относящийся к мышлению), но и онтологический (относящийся к бытию) смысл: «… ни одно явление не может оказаться истинным или действительным, ни одно утверждение справедливым, — без достаточного основания, почему именно дело обстоит так, а не иначе…»)^[16][18]; Лейбниц является также автором современной формулировки закона тождества^[5][8][17]; он ввёл 

термин «модель»^[5], писал о возможности машинного моделирования функций человеческого мозга^[19]. Лейбниц высказал идею о превращении одних видов энергии в другие^[5], сформулировал один из важнейших вариационных принципов физики — «принцип наименьшего действия» — и сделал ряд открытий в специальных разделах физики^[5][8].

Он первым обратился к вопросу о возникновении российской правящей династии^[20], первым в немецкой историографии обратил внимание на взаимосвязь лингвистических проблем с генеалогией^[20], создал теорию исторического происхождения языков и дал их генеалогическую классификацию, явился одним из создателей немецкого философского и научного лексикона^[5][8].

Лейбниц также ввёл идею целостности органических систем, принцип несводимости органического к механическому и высказал мысль об эволюции Земли^[5].

Дави́д Ги́льберт (нем. David Hilbert; 23 янв

аря 1862 — 14 февраля 1943) — немецкий математик-универсал, внёс значительный вклад в развитие многих областей математики. В 1910—1920-е годы (после смерти Анри Пуанкаре) был признанным мировым лидером математиков. Гильберт разработал широкий спектр фундаментальных идей во многих областях математики, в том числе теорию инвариантов и аксиоматику евклидовой геометрии. Он сформулировал теорию гильбертовых пространств, одну из основ современного функционального анализа^[4].

Английский математик и логик. Профессор математики Королевского колледжа Корка с 1849 года. Один из основателей математической логики. Буль был, вероятно, первым после Джона Валлиса математиком, обратившимся к логической проблематике. Буль не считал логику разделом математики, но находил глубокую аналогию между символическим методом алгебры и символическим методом представления логических форм и силлогизмов.На математические темы Булем в течение жизни были созданы два систематических трактата: «Трактат о дифференциальных уравнениях» (1859; второе издание не завершено, материалы к нему опубликованы посмертно в 1865) и задуманный как его продолжение «Трактат о конечных разностях» (1860). Эти труды внесли важный вклад в соответствующие разделы математики и в то же время продемонстрировали глубокое понимание Булем философии своего предмета.

Дизъю́нкция (лат. disjunctio — разобщение), логи́ческое сложе́ние, логи́ческое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу»

|| b,a{\displaystyle b,\;a} | b,a ORb{\displaystyle b,\;a~{\mbox{OR}}\,\,b},max(a,b).{\displaystyle ,\;\max(a,b).}

Закон, выражающий дистрибутивность (распределительность) одной данной логической или математической операции относительно другой данной операции. Примером этого закона может служить закон обычной арифметики: а (b + с) = аb + ас, выражающий распределительность умножения относительно сложения.

Формула закона:

.

.
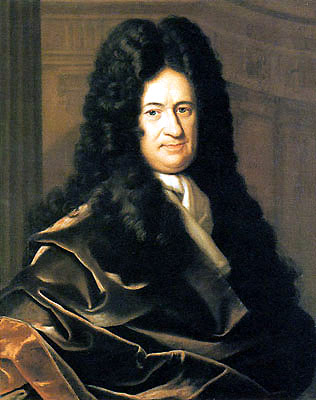